
One of the biggest challenges of building a statistical model is deciding which model to use. The following table contains a data set with the weight and height of ten.
#Residual statistics download#
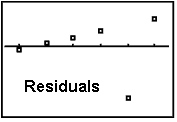
Therefore the residual for the 59 inch tall mother is 0.04. Download Table z i Statistics for Residual Means, Z ij Statistics for Residual Cross-Products, and Residual Correlations After Fitting a Graded Response. What Is a Residual in Stats Example and Practice Finding Residuals. Reading Q-Q plots, is a bit of an art, not completely a science.= y-\hat y = 61-60.96=0.04\nonumber \] (If these were residuals of a model.) For sample sizes of 10 and 25 we may be suspicious, but not entirely confident. So for the sample size of 100, we would conclude that the normality assumption is violated. This indicates that the values are too small (negative) or too large (positive) compared to what we would expect for a normal distribution. While many of the points are close to the line, at the edges, there are large discrepancies. The greater the absolute value of the residual, the further that the point lies from the regression line. This affects inference but not point estimates of the. The residual plots reflect that the assumptions of residual normality and homogeneity are violated. Here, using 4 degrees of freedom, we have a distribution that is somewhat normal, it is symmetrical and roughly bell-shaped, however it has “fat tails.” This presents itself clearly in the third panel. Residuals are zero for points that fall exactly along the regression line. Cross Validated is a question and answer site for people interested in statistics, machine learning, data analysis, data mining, and data visualization. Recall that as the degrees of freedom for a \(t\) distribution become larger, the distribution becomes more and more similar to a normal. Hypothesis tests will then accept or reject incorrectly. The distributions of the parameter estimates will not be what we expect. A residual plot is a graph that shows the residuals on the vertical axis and the independent variable on the horizontal axis. If these assumptions are not met, we can still “perform” a \(t\)-test using R, but the results are not valid. If these assumptions are met, great! We can perform inference, and it is valid. Since the \(\epsilon_i\) are \(iid\) normal random variables with constant variance. Given a data point and the regression line, the residual is defined by the vertical difference between the observed value of y and the computed value of y based on the equation of the regression line: Residual y y. 3) Example 2: Compute Summary Statistics of Residuals Using summary () Function. 2) Example 1: Extracting Residuals from Linear Regression Model. Table of contents: 1) Introduction of Example Data.
#Residual statistics how to#
While the remaining three, are all encoded in In the linear regression part of statistics we are often asked to find the residuals. This tutorial shows how to return the residuals of a linear regression and descriptive statistics of the residuals in R. Recall the multiple linear regression model that we have defined. 17.3.6 Confidence Intervals for Mean Response Compute the residuals for the observations (85.0, 98.6) ('+' in Figure 7.2.16 Variable Selection and Model Building.14.2.5 poly() Function and Orthogonal Polynomials.14.1.1 Variance Stabilizing Transformations.11.3.1 Factors with More Than Two Levels.


 0 kommentar(er)
0 kommentar(er)
